近日,苏州大学物理科学与技术学院冯岩教授团队与合作者系统地研究了二维简单液体的基础物性,首次给出其剪切黏度在单原子层面的解析公式,并利用计算机模拟不同作用势的液体验证了此公式的普适性。该项研究利用“跳越”模型描述液体复杂的微观动力学过程,为液体剪切黏度微观机制的深入理解提供了全新的物理图像。相关成果以“Atomistic mechanisms of viscosity in 2D liquid-like fluids”为题发表在《Nature Communications》上,原文链接:https://doi.org/10.1038/s41467-025-65246-5。
当蜂蜜缓缓流出汤匙,当机油在引擎内承受高温,人们习以为常的“黏稠”背后究竟发生了什么?自牛顿1687年在《自然哲学的数学原理》中写下剪切应力与剪切速率的比例关系,黏度便成为描述流体力学的基石概念之一,然而,这一宏观表达式并未触及其微观物理图像。气体可用动理论描述,即原子(或分子,下同)碰撞传递动量,黏度与温度平方根成正比;但液体原子密集,相互作用势场重叠,导致传统的原子碰撞的物理图像失效。20世纪30年代,Eyring提出化学动力学形式的黏度公式,却留下预因子与活化能两个待定参数。随后40年代,Frenkel将液体原子的运动视为短时间类似固体原子振动与长时间在局部势阱间跳跃这两种运动的综合,这虽然给出了直观的物理图像,但却未能给出定量化的参量。此后约八十年,作为流体输运系数,液体黏度的微观表达式始终“缺席”,液体复杂的微观结构和集体动力学使得理论计算其黏度的努力一直步履维艰。诺贝尔奖得主温伯格曾一针见血地指出:计算水的黏度,其难度堪比推演塑造宇宙的基本常数。朗道也曾说:几乎不可能推导出任何能定量描述液体性质的一般公式。因此,液体的黏度微观机制至今仍是困扰科学界的谜题之一。
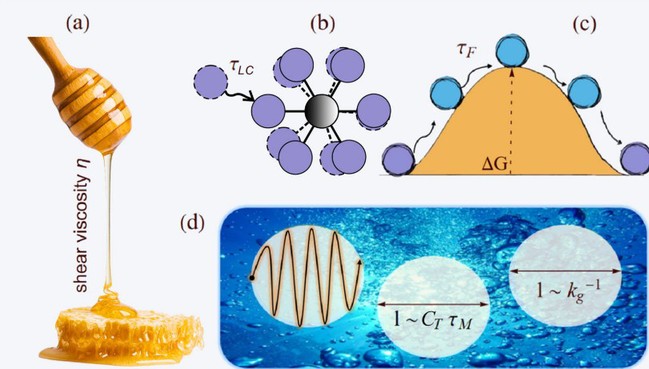
图1:液体黏度、原子运动和剪切波传播示意图
本项研究工作化繁为简,将每个原子失去或获得一个最近邻的平均时间,这一较容易观测的拓扑事件,定义为局域连通寿命\tau _{LC}。团队通过将Frenkel的液体描述与原子局域连通寿命相结合,理论推导出二维液体黏度等于质量密度、颗粒平均速率的平方、局域连通寿命三者之积,再乘以一个与系统相互作用相关并趋近于1的系数。为了验证这一公式的普适性,团队在三种相互作用迥异的二维液体系统(Lennard-Jones,Yukawa,Coulomb)中进行了不同参数条件下的大规模模拟和数据分析。研究结果显示,尽管这些系统的相互作用从短程吸引排斥的Lennard-Jones到中程Yukawa排斥,甚至到长程的库仑排斥各不相同,但不同参数下三类液体的黏度均准确地落在了上述黏度的解析表达式,如图2所示。
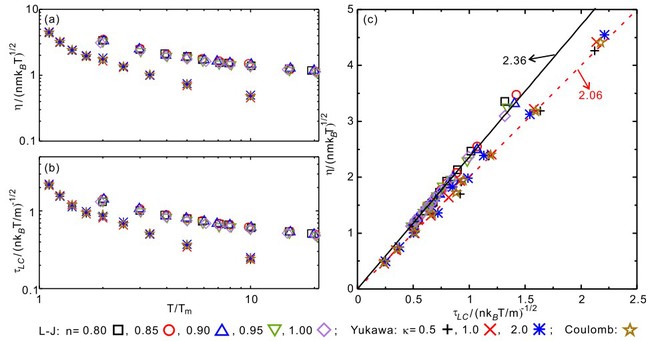
图2:二维简单液体黏度和局域连通寿命的关系
更令人兴奋的是,团队成功地从液体最基本的静态结构,径向分布函数g(r)中,提取出决定系统局域连通寿命而需要克服的势垒信息。研究结果显示,二维简单液体的\tau_{LC}仅由径向分布函数g(r)的第一个峰和第一个谷的高度差所决定,即系统局域连通寿命等于高温极限类气体状态的局域连通寿命,再乘以径向分布函数第一个峰和第一个谷高度之比。将该结果代入Frenkel的液体描述中,最终解析推导出了二维液体剪切黏度和系统原子排布结构之间的关联,如图3所示,即黏度等于高温极限类气体状态黏度再乘以径向分布函数第一个峰和第一个谷高度之比,该结果意味着可以通过液体系统的原子排布结构来准确预测其剪切黏度。
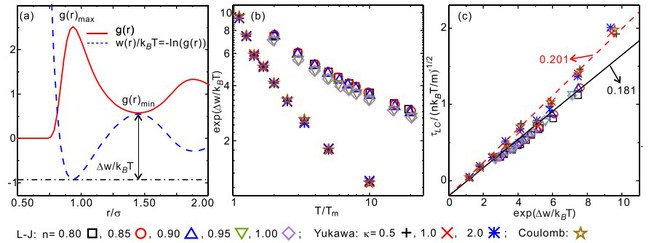
图3:二维简单液体局域连通寿命和原子排布结构的关系
这项研究成果将液体输运系数这一宏观物理量与该系统原子层面的微观参数直接联系起来,由此可通过追踪液体系统单原子层面“网络”结构变化的快慢,有效预测系统整体的物理性质。该研究巧妙地融合了液体理论、黏弹性理论,以及液体黏度Eyring模型这几类液体理论框架,为未来研究液体其它物理性质提供了全新的研究范式。
苏州大学黄栋副教授是该论文的第一作者,苏州大学冯岩教授和上海交通大学Matteo Baggioli教授是该论文的通讯作者。该研究获得国家自然科学基金委的资助,同时得到苏州大学物理科学与技术学院的支持。


